Here’s the equation we settled upon. I’ve yet to have time to graphically model this in software like MatLab so if any
readers are mathematically inclined (I left maths behind after Fourier and Laplace mathematics at university), I’d love
to see if we can construct a graphical representation of this.
But first, some acronyms:
¡ì OSH: Optimal Sock height. The height at which we posit that one’s peak cycling performance is attained.
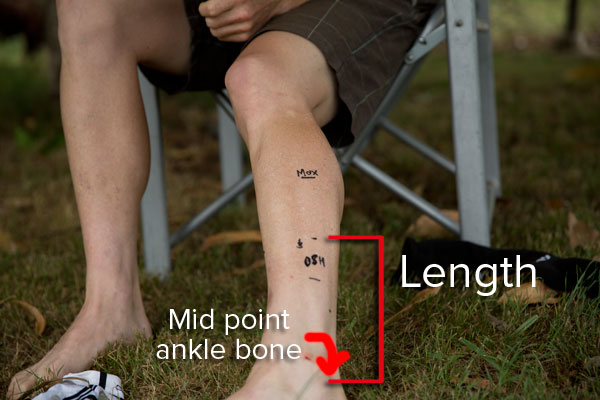
¡ì SHmin: Sock Height Minimum. The height on the calf, for your minimum sock height. Measured from the midpoint on
your ankle bone.
¡ì SHmax: Sock Height Minimum. The height on the calf, for your minimum sock height. Measured from the midpoint on
your ankle bone.
¡ì CLmin and CLmax: the minimum and maximum cuff lengths for the actual sock. These are normally the length the
socks are sold at, for example, Swiftwick’s 4¡å cuff would be a 10cm cuff.
¡ì H, or h, is your height, measured in centimetres, and expressed in decimal number. This means a height of 187cm
would give h=1.87.
First we can posit that OSH can be described as a relationship between SHmin and SHmax, with the OSH initially being
described thus:
OSH= ½(SHmax-SHmin)
We therefore can see we need to solve for SHmax and SHmin.
After performing some sock height optimising investigations (in the video), I came up with a formula.
These equations are normalised to my height, however they do include adjustments for your height, and also,
importantly Q factor, or Cankle Quotient.
I am still trying to find an objective ratio to describe Q factor, but it currently can be described as lying between 0.5
and 1.
If you have almost zero cankle factor, your Q will be 1. If you are very cankly you will want to use Q=0.5.
I welcome any improvements on this methodology.
Minimum and maximum sock heights are solved in a similar fashion as shown below£¨in next article£©.